Brain Gains (Rapid Recall, Jivin' Generation)

- Consider the region $R$ in the first quadrant that lies above the curves $y=x$ and $y=\frac{1}{x}$, and below the curves $y=3x$ and $y=\frac{4}{x}$. Note that we can rewrite $x\leq y\leq 3x$ as $1\leq \frac{y}{x}\leq 3$, and we can rewrite $\frac{1}{x}\leq y\leq \frac{4}{x}$ as $1\leq xy\leq 4$. Using the change-of-coordinates $u = xy$ and $v=\frac{y}{x}$, compute the integral $\ds\iint_R dA$.
Solution
Computing differentials gives us $$\begin{pmatrix}du\\dv\end{pmatrix} = \begin{pmatrix}y\\-y/x^2\end{pmatrix}dx+\begin{pmatrix}x\\1/x\end{pmatrix}dy = \begin{bmatrix}y&x\\-y/x^2&1/x\end{bmatrix}\begin{pmatrix}dx\\dy\end{pmatrix}.$$ The Jacobian of the transformation is $$\frac{\partial (u,v)}{\partial(x,y)} = |(y)(1/x) - (-y/x^2)(x)| = |2(y/x)| = |2v| = 2v.$$ We need $\ds \frac{\partial (x,y)}{\partial(u,v)} = \frac{1}{2v},$ which gives $$\iint_R dA = \iint \frac{\partial (x,y)}{\partial(u,v)} dudv = \int_{1}^{3}\int_{1}^{4}\frac{1}{2v}dudv.$$ Software can quickly compute this integral. Here is some Mathematica code that draws the region, and then computes the integral in three different ways.
R = ImplicitRegion[1 <= x y <= 4 && 1 <= y/x <= 3 && x >= 0, {x, y}]
Show[Plot[{1/x, 4/x, 3 x, x}, {x, 0, 4}, PlotRange -> {0, 4}], Region[R]]
(*Integrate using the change-of-coordiantes.*)
Integrate[1/(2 v), {v, 1, 3}, {u, 1, 4}] // N
(*Integrate using Mathematica's region utilities.*)
Integrate[1, {x, y} \[Element] R] // N
(*Compute the integral by splitting the region up into 3 Cartesian regions.*)
Integrate[1, {x, Sqrt[1/3], 1}, {y, 1/x, 3 x}] +
Integrate[1, {x, 1, Sqrt[4/3]}, {y, x, 3 x}] +
Integrate[1, {x, Sqrt[4/3], 2}, {y, x, 4/x}] // N
Here is a way to visualize the region that shows the images of 1 by 1 boxes from the $uv$-plane, and 1/4 by 1/4 boxes, so we can visualize what the Jacobian $\frac{1}{2v}$ actually means.
coordinates = {Sqrt[u /v], Sqrt[u v]};
ParametricPlot[Evaluate[coordinates, {u, 1, 4}, {v, 1, 3}], Mesh -> 1 {3, 2} - {1, 1}]
coordinates = {Sqrt[u /v], Sqrt[u v]};
ParametricPlot[Evaluate[coordinates, {u, 1, 4}, {v, 1, 3}], Mesh -> 4 {3, 2} - {1, 1}]
- Consider the region $R$ that lies inside the triangle with vertices $(0,1)$, $(1,-2)$, and $(2,3)$, and the change-of-coordinates $u=x-y+1$, $v=3x+y-1$. (These coordinates were obtained by finding an equation of the lines of two edges of the triangle.) Show that $\ds \frac{\partial (x,y)}{\partial(u,v)} = \frac{1}{4}$, and then fill in the missing bounds of the integral $$\ds\iint_R 3x+y dA = \int_{0}^{?}\int_{0}^{?}(v+1)(\frac{1}{4})dvdu.$$
Solution
The Jacobian of $u$ and $v$ with respect to $x$ and $y$ is the area of the parallelogram with edges equal to $\frac{\partial (u,v)}{\partial x}=(1,3)$ and $\frac{\partial (u,v)}{\partial y}=(-1,1)$, which is $A = |(1)(1)-(3)(-1)|=4$. This gives $\ds \frac{\partial (u,v)}{\partial(x,y)} = 4$, and hence we have $\ds \frac{\partial (x,y)}{\partial(u,v)} = \frac{1}{4}$.
To find the bounds, we need to figure out where the points $(0,1)$, $(1,-2)$, and $(2,3)$ lie in the $(u,v)$ plane.
- The point $(x,y)=(0,1)$ is at $u=0-1+1 = 0$ and $v=3(0)+1-1 = 0$, so $(u,v)=(0,0)$, the origin of our new coordinate system.
- The point $(x,y)=(1,-2)$ is at $u=1-(-2)+1 = 4$ and $v=3(1)+(-2)-1 = 0$, so $(u,v)=(4,0)$.
- The point $(x,y)=(2,3)$ is at $u=2-(3)+1 = 4$ and $v=3(2)+(3)-1 = 0$, so $(u,v)=(0,8)$.
The three points form a triangle in the $uv$-plane. The top edge of that triangle is the line $v=8-2u$. As such, we have $$\ds\iint_R 3x+y dA = \int_{0}^{4}\int_{0}^{8-2u}(v+1)(\frac{1}{4})dvdu.$$
coordinates = {(u + v)/4, (v - 3 u + 4)/4};
ParametricPlot[Evaluate[coordinates, {u, 0, 4}, {v, 0, 8 - 2 u}], Mesh -> {10, 0}]
- A bead is formed by drilling a hole through a sphere. The solid region shown below is the region inside a sphere of radius 2 and outside a cylinder of radius 1. Set up an iterated triple integral in spherical coordinates that would give the volume of the solid.
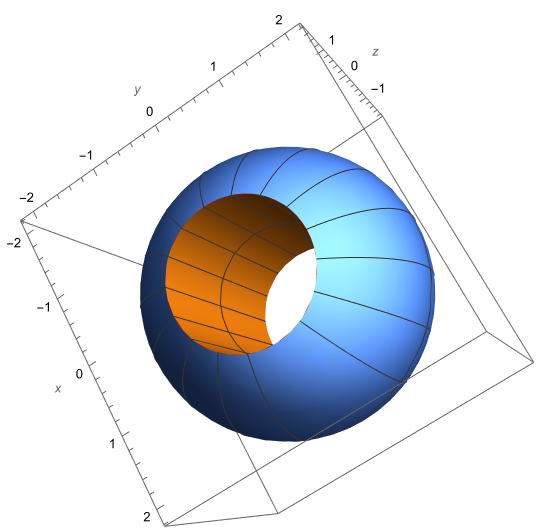
Solution
The sphere has equation $\rho = 2$. The cylinder has equation $r=1$ or rather $\rho \sin \phi = 1$, which we can rewrite at $\rho = \csc \phi$. The two surfaces intersect when $\sin\phi = \frac{1}{2}$, so when $\phi = \pi/6$ and $\phi = 5\pi/6$. The volume is given by the integral $$V=\int_{0}^{2\pi}\int_{\pi/6}^{5\pi/6}\int_{\csc \phi}^{2}\rho^2\sin\phi d\rho d\phi d\theta.$$
We can check our solution is correct by drawing the region with Mathematica. The code below uses the custom function plotRegion3D[]. You can also use the built in ParametricRegion[] command (see a previous day for examples).
plotRegion3D[cs_, ob_, mb_, ib_] :=
Show[{{ParametricPlot3D[Evaluate[Table[cs /. (ib[[1]] -> ib[[i]]), {i, 2, 3}], ob, mb], AxesLabel -> {x, y, z}, Mesh -> {15, 1}],
ParametricPlot3D[Evaluate[Table[(cs /. (ib[[1]] -> (ib[[2]] (1 - s) + ib[[3]] s))) /. (mb[[1]] -> mb[[i]]), {i, 2, 3}], ob], {s, 0, 1}, PlotStyle -> {Red, Blue}, Mesh -> {15, 0}],
ParametricPlot3D[Evaluate[Table[(cs /. (ib[[1]] -> (ib[[2]] (1 - s) + ib[[3]] s))) /. (mb[[1]] -> (mb[[2]] (1 - t) + mb[[3]] t)) /. (ob[[1]] -> ob[[i]]), {i, 2, 3}]], {t, 0, 1}, {s, 0, 1}, PlotStyle -> Green, Mesh -> {0, 0}]}}, PlotRange -> All]
coordinates = {rho Sin[phi] Cos[theta], rho Sin[phi] Sin[theta], rho Cos[phi]}
plotRegion3D[coordinates, {theta, 0, 2 Pi}, {phi, Pi/6, 5 Pi/6}, {rho, Csc[phi], 2}]
- Consider the 2D region in the $yz$-plane satisfying $1\leq y \leq 2$ and $y\leq z\leq 9-y^2$. This region is revolved about the $z$-axis to produce a solid of revolution. Set up a triple integral in cylindrical coordinates that would give the volume of this solid. Half of the region is shown below.
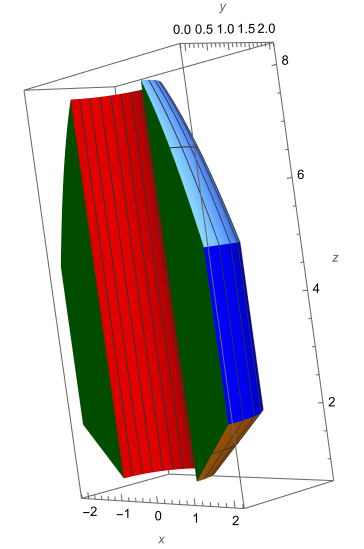
Solution
The volume is $$V=\int_{0}^{2\pi}\int_{1}^{2}\int_{r}^{9-r^2}r dz dr d\theta.$$
We can check our solution is correct by drawing the region with Mathematica, using the custom function plotRegion3D[] (defined in the previous question).
coordinates = {r Cos[theta], r Sin[theta], z}
plotRegion3D[coordinates, {theta, 0, 2 Pi}, {r, 1, 2}, {z, r, 9-r^2}]
Group Problems
- Consider the solid of revolution obtained by revolving about the $z$-axis the 2D region in the $xz$-plane that lies below the line $z = 4-x$ for $2\leq x\leq 4$.
- Set up an iterated triple integral in cylindrical coordinates using the order $d\theta dz dr$ that would give the volume of this solid.
- Set up an iterated triple integral in cylindrical coordinates using the order $d\theta dr dz$ that would give the volume of this solid.
- Use Mathematica to verify that the bounds you gave do indeed correctly describe the solid.
- Compute one of the integrals above by hand (feel free to check with software).
- Consider the region $R$ in the plane that lies inside the triangle with corners $(0,0)$, $(1,2)$, and $(-3,1)$. Two edges are given by the lines $2x-y=0$ and $x+3y=0$, so let's use the change-of-coordinates $u=2x-y$ and $v=x+3y$.
- Compute $\ds \frac{\partial (u,v)}{\partial(x,y)}$ and $\ds \frac{\partial (x,y)}{\partial(u,v)}$.
- Draw the region $R$ in the $uv$-plane.
- Use the change-of-coordinates to set up an appropriate integral in terms of $u$ and $v$ to compute $\iint_R xy dA$.
- Consider the vector field $\ds \vec F = \frac{1}{2\pi}\left(\frac{-y}{x^2+y^2},\frac{x}{x^2+y^2}\right)$.
- Let $C$ be the curve parametrized by $\vec r(t) = (3\cos t, 3\sin t)$ for $0\leq t\leq 2\pi$. Compute the work done by $\vec F$ to move an object along $C$. [Hint: The answer is NOT zero.]
- Let $C$ be the curve parametrized by $\vec r(t) = (7\cos t, 7\sin t)$ for $0\leq t\leq 4\pi$. Compute the work done by $\vec F$ to move an object along $C$.
- Let $C$ be the curve parametrized by $\vec r(t) = (a\cos t, a\sin t)$ for $0\leq t\leq 2k\pi$. Compute the work done by $\vec F$ to move an object along $C$.
- Show that $D\vec F(x,y)$ is symmetric.
- Does $\vec F$ have a potential?
Solutions
If $\vec F$ had a potential, then the work done along a closed curve would be zero. This is not true, as the first 3 parts illustrate. The vector field does NOT have a potential.
The function and derivative are not defined at $(0,0)$, which means the domain of the vector field is not simply connected. We cannot use the symmetry of the derivative to conclude that there is a potential, because the domain is not simply connected.
Here are some Mathematica computations relevant to this problem.
ClearAll[F, r]
F[x_, y_] := 1/(2 Pi (x^2 + y^2)) {-y, x}
r[t_] := {a Cos[t], a Sin[t]}
(*Is the derivative symmetric*)
D[F[x, y], {{x, y}}] // Simplify // MatrixForm
(*Try to find a potential*)
Integrate[F[x, y][[1]], x]
Integrate[F[x, y][[2]], y]
(*Compute work done by wrapping k times around a circle of radius a*)
Dot[F @@ r@t, D[r[t], t]] // Simplify
Integrate[Dot[F @@ r@t, D[r[t], t]], {t, 0, 2 k Pi}]
