Brain Gains (Rapid Recall, Jivin' Generation)

- Consider the vector field $\vec F(x,y,z) = (2x+3z, 4y,3x-3z^2)$ and the helical curve $C$ parametrized by $\vec r(t) = (t, \cos (\pi t), \sin(\pi t))$ for $0\leq t\leq 2$.
- Find a potential for $\vec F$.
- Find work done by $\vec F$ to move an object along $C$.
Soluiton
A potential is $f(x,y,z) = x^2 + 3xz +2y^2-z^3$. The start point on the curve is $A = \vec r(0)=(0,1,0)$ and the end point is $B = (2,1,0)$, The work done along the curve is $$\int_C \vec F \cdot d\vec r = f(B)-f(A) = (4+2)-(2)=4.$$
ClearAll[F, f, r, potential]
F[x_, y_, z_] := {2 x + 3 z, 4 y, 3 x - 3 z^2}
sol = DSolve[D[f[x, y, z], {{x, y, z}}] == F[x, y, z], f, {x, y, z}] //Flatten
potential = f /. sol;
(*Manually type in the end points*)
potential[2, 1, 0] - potential[0, 1, 0]
(*Use function notation to evaluate the potential at the end points.*)
r[t_] := {t, Cos[Pi t], Sin[Pi t]}
potential @@ r@2 - potential @@ r@0
(*The apply function (@@) is required for function composition when the output is a vector.*)
(*Here we compute work using the formula from earlier in the semester*)
Integrate[Dot[Apply[F, r[t]], D[r[t], t]], {t, 0, 2}]
Integrate[Dot[F @@ r@t, r'@t], {t, 0, 2}]
- Consider the integral $\iint_RdA$, the region satisfying $-1\leq x+y\leq 4$ and $0\leq 2x-y\leq 3$, and the change-of-coordinates $u=x+y$ and $v=2x-y$.
- Draw the region $R$.
- Compute the Jacobians $\dfrac{\partial(u,v) }{\partial (x,y) }$ and $\dfrac{\partial(x,y) }{\partial (u,v) }$.
- Fill in the missing part of $\ds \iint_RdA = \int_{-1}^{4}\int_{0}^{3}?dvdu$, and then evaluate the integral.
- Try solving $\ds \iint_RxdA$, using the change-of-coordinates. What missing information will you need to find?
Solution
- The region is a parallelogram.
- The Jacobians are $\dfrac{\partial(u,v) }{\partial (x,y) } =\left|1(-1)-1(2)\right|= 3$ and $\dfrac{\partial(x,y) }{\partial (u,v) }=\frac{1}{3}$.
- The integral is $\ds \iint_RdA = \int_{-1}^{4}\int_{0}^{3}\dfrac{\partial(x,y) }{\partial (u,v) }dvdu = \int_{-1}^{4}\int_{0}^{3}\frac{1}{3}dvdu$.
- We need to solve for $x$ in terms of $u$ and $v$. For this particular problem, we can do that by simply adding the two equations $u=x+y$ and $v=2x-y$ together, which gives $u+v=3x$. Division by 3 yields $x = \frac{u+v}{3}$. We then have $\ds \iint_RxdA = \int_{-1}^{4}\int_{0}^{3}\frac{u+v}{3}\frac{1}{3}dvdu$.
Here are two ways to draw the region in Mathematica. The first skips entirely the change-of-coordinates, while the latter solves for $x$ and $y$ in terms of $u$ and $v$ first, and then uses the change of coordinates.
coordinates = {x, y}
R = ParametricRegion[{coordinates, -1 <= x + y <= 4 && 0 <= 2 x - y <= 3}, {x, y}];
Region[R, Axes -> True, AxesLabel -> {x, y}, AxesOrigin -> {0, 0}]
coordinates = {(u + v)/3, (2 u - v)/3}
R = ParametricRegion[coordinates, {{u, -1, 4}, {v, 0, 3}}];
Region[R, Axes -> True, AxesLabel -> {x, y}, AxesOrigin -> {0, 0}]
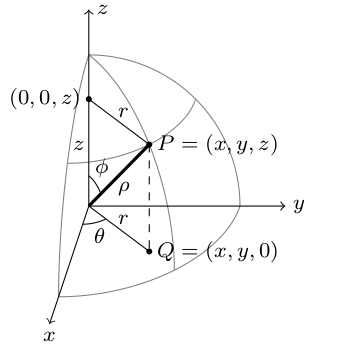
- Give the $(x,y,z)$ coordinates of the point in space whose spherical coordinates are $(\rho,\phi,\theta) = (3,\pi/2,\pi)$.
Solution
We're on a sphere of radius $rho =3$. The fact that $\phi=\pi/2$ means we've dropped 90 degrees from the positive $z$-axis, so we are in the $xy$-plane. With an angle of $\theta=\pi$, that puts us on the negative $x$-axis. The solution is $$(x,y,z)=(-3,0,0).$$
- Give $(\rho,\phi,\theta)$ coordinates for the Cartesian coordinates $(0,0,4)$, $(3,0,0)$, $(0,2,0)$, and $(0,0,-1)$.
Solution
A solution appears in the table below. When $\phi=0$ or $\phi=\pi$, the value of $\theta$ is arbitrary. You can of course add any multiple of $2\pi$ to any value of $\theta$ below, and still have a valid solution. $$\begin{array}{c|c} \text{Cartesian}&\text{Spherical}\\ (x,y,z)&(\rho,\phi,\theta)\\\hline (0,0,4)& (4,0,\text{any})\\ (3,0,0)& (3,\pi/2,0)\\ (0,2,0)& (2,\pi/2,\pi/2)\\ (0,0,-1)&(1,\pi,\text{any}) \end{array}$$
- Draw the region in space whose volume is computed from the triple integral $$\ds \int_{0}^{\pi}\int_{\pi/4}^{\pi/2}\int_{0}^{3}\rho^2\sin\phi d\rho d\phi d\theta.$$
Solution
coordinates = {rho Sin[phi] Cos[theta], rho Sin[phi] Sin[theta], rho Cos[phi]}
R = ParametricRegion[coordinates, {{rho, 0, 3}, {phi, Pi/4, Pi/2}, {theta, 0, Pi}}];
Region[R, Axes -> True, AxesLabel -> {x, y, z}, AxesOrigin -> {0, 0, 0}]
Group Problems
- Compute the work done by the vector field $\vec F = (4x+2xy,x^2+2y)$ along the curve $C$ parametrized by $\vec r(t) = (3t-1,-5t+2)$ for $0\leq t\leq 1$. [Hint: First find a potential.]
Solution
The vector field has a potential as the derivative $D\vec F =\begin{bmatrix}- &2x \\2x &-\end{bmatrix}$ is symmetric.
- A potential for the vector field is $f(x,y) = 2x^2+x^2y+y^2$ (note $\int 4x+2xy dx = 2x^2+x^2y +C(y)$ and $\int x^2+2y dy = x^2y+y^2+D(x)$).
- The start point is $\vec r(0) = (-1,2)$ and the end point is $\vec r(1) = (2,-3)$.
The work done by $\vec F$ is the difference in potential, which gives $$\int_C\vec F\cdot d\vec r = f(2,-3) - f(-1,2)=(8-12+9)-(2+2+4) = 5-8 = - 3.$$
- Draw the region in space described by $1\leq r \leq 3$, $\pi/2\leq \theta \leq \pi$, $0\leq z\leq 4$. In other words, draw the region in space whose volume is given, in cylindrical coordinates, by the iterated triple integral
$$\int_{1}^{3}\int_{\pi/2}^{\pi}\int_{0}^{4}rdz d\theta dr.$$
Solution
coordinates = {r Cos[theta], r Sin[theta], z}
R = ParametricRegion[coordinates, {{r, 1, 3}, {theta, Pi/2, Pi}, {z, 0, 4}}];
Region[R, Axes -> True, AxesLabel -> {x, y, z}, AxesOrigin -> {0, 0, 0}]
- Set up an integral formula to compute $\bar x$ for the solid above (use cylindrical coordinates).
Solution
No density is given, which means we interpret $\bar x$ as the $x$-coordinate of the centroid (so center of mass with $\delta=1$). This gives $$\bar x = \frac{\iiint_DxdV}{\iiint_DdV} = \frac{\ds\int_{1}^{3}\int_{\pi/2}^{\pi}\int_{0}^{4}(r\cos\theta)rdz d\theta dr}{\ds\int_{1}^{3}\int_{\pi/2}^{\pi}\int_{0}^{4}rdz d\theta dr}.$$
- Give cylindrical equations for both the the sphere $x^2+y^2+z^2=9$ and paraboloid $z=9-x^2-y^2$.
Solution
Recall that $x^2+y^2=r^2$.
- An equation for the sphere is $r^2+z^2=9$.
- An equation for the paraboloid is $z=9-r^2$.
- The spherical change-of-coordinates is given by $$(x,y,z) = (\underbrace{\rho\sin\phi}_{r}\cos\theta, \underbrace{\rho\sin\phi}_{r}\sin\theta, \rho\cos\phi).$$
- Give Cartesian coordinates $(x,y,z)$ for the spherical coordinates $(\rho,\phi,\theta)$ given by $(2,\pi/2,\pi)$, $(2,\pi,\pi/2)$, and $(2,0,3\pi)$.
- Explain why an equation of the sphere $x^2+y^2+z^2=9$ in spherical coordinates is $\rho = 3$.
- Explain why an equation of the cone $x^2+y^2=z^2$ (so $r^2=z^2$ or $r=z$) in spherical coordinates is $\phi = \pi/4$.
- Set up an integral to find the volume of the region in space above the $xy$-plane that is bounded above by the sphere $x^2+y^2+z^2=9$ and below by the cone $z^2=x^2+y^2$. The Jacobian for spherical coordinates is $|\rho^2\sin\phi|$.
- You can check your solution with Mathematica by updating the code below.
coordinates = {rho Sin[phi] Cos[theta], rho Sin[phi] Sin[theta], rho Cos[phi]} R = ParametricRegion[coordinates, {{rho, 0, 3}, {phi, Pi/4, Pi/2}, {theta, 0, Pi}}]; Region[R, Axes -> True, AxesLabel -> {x, y, z}, AxesOrigin -> {0, 0, 0}]
- You can check your solution with Mathematica by updating the code below.
- Explain why an equation of the plane $z=8$ in spherical coordinates is $\rho = 8\sec \phi$.
- Set up an integral to find the volume of the region in space above the $xy$-plane that is bounded above by the plane $z=8$ and below by the cone $z^2=x^2+y^2$. Check your work with Mathematica.
Some Solutions
Here is the region for part d.
coordinates = {rho Sin[phi] Cos[theta], rho Sin[phi] Sin[theta], rho Cos[phi]}
R = ParametricRegion[coordinates, {{theta, 0, 2 Pi}, {phi, 0, Pi/4}, {rho, 0, 3}}];
Region[R, Axes -> True, AxesLabel -> {x, y, z}, AxesOrigin -> {0, 0, 0}]
The corresponding integral is $$V=\int_{0}^{2\pi}\int_{0}^{\pi/4}\int_{0}^{3}\rho^2\sin\phi d\rho d\phi d\theta.$$
Integrate[rho^2 Sin[phi], {theta, 0, 2 Pi}, {phi, 0, Pi/4}, {rho, 0, 3}]
Here is the region for part f.
coordinates = {rho Sin[phi] Cos[theta], rho Sin[phi] Sin[theta], rho Cos[phi]}
R = ParametricRegion[coordinates, {{theta, 0, 2 Pi}, {phi, 0, Pi/4}, {rho, 0, 8/Cos[phi]}}];
Region[R, Axes -> True, AxesLabel -> {x, y, z}, AxesOrigin -> {0, 0, 0}]
The corresponding integral is $$V=\int_{0}^{2\pi}\int_{0}^{\pi/4}\int_{0}^{8/ \cos\phi}\rho^2\sin\phi d\rho d\phi d\theta.$$
Integrate[rho^2 Sin[phi], {theta, 0, 2 Pi}, {phi, 0, Pi/4}, {rho, 0, 8/Cos[phi]}]
