Brain Gains (Rapid Recall, Jivin' Generation)

- For the function $f(x,y)=x^2+4xy+3y^2-10x-18y$, find the critical points.
Solution
The only critical point is $(x,y)=(3,1)$.
The first derivative is $$Df(x,y) = \begin{bmatrix}2x+4y-10&4x+6y-18\end{bmatrix}.$$ To find the critical points, we need this derivative to be the zero matrix, which means we must solve the system of equations $$ 2x+4y-10 = 0,\quad 4x+6y-18=0.$$ This is equivalent to solving $2x+4y=10$ and $4x+6y=18$. Dividing both sides of the second equation by 2 gives the system $2x+4y=10$ and $2x+3y=9$. Subtracting the second equation from the first yields $y=1$, and substitution into either equation yields $x=3$.
- For the function $f(x,y) = x^3+3xy+y^3$, the first and second derivatives are $$Df(x,y) = \begin{bmatrix}3x^2+3y&3x+3y^2\end{bmatrix}\quad\text{and}\quad D^2f(x,y) = \begin{bmatrix}\begin{matrix}6x\\3\end{matrix}&\begin{matrix}3\\6y\end{matrix}\end{bmatrix}. $$ A critical point of the function is $(x,y)=(-1,-1)$, which we can verify by computing $$Df(-1,-1) = \begin{bmatrix}3(-1)^2+3(-1)&3(-1)+3(-1)^2\end{bmatrix} = \begin{bmatrix}0&0\end{bmatrix}.$$ Does the function have a maximum or minimum at this critical point? Use the eigenvalues of $D^2f(-1,-1)$ to explain.
Solution
Note that $D^2f(-1,-1) = \begin{bmatrix}\begin{matrix}-6\\3\end{matrix}&\begin{matrix}3\\-6\end{matrix}\end{bmatrix}.$ We find the eigenvalues by solving $(-6-\lambda)(-6-\lambda)-(3)(3) = 0$. This is equivalent to solving $$0=\lambda^2+12\lambda+36-9 = \lambda^2+12\lambda+27 = (\lambda+9)(\lambda+3).$$ The eigenvalues of $D^2f(-1,-1)$ are $\lambda = -9$ and $\lambda = -3$, both of which are negative. We have already seen that negative eigenvalues mean the gradient field points inwards, meaning the critical point $(-1,-1)$ is the location of a local maximum. We can verify all these facts using the following Mathematica notebook.
- A rover travels along the path $2x-4y=12$. The elevation is given by $z=x+y^2-3$. Use Lagrange multipliers to find the $(x,y)$ location of the lowest elevation reached by the rover along this path.
Solution
The solution is $(x,y)=(4,-1)$.
To use Lagrange multipliers, remember you need to identify
- $f(x,y)$ - the thing you wish to optimize - $f(x,y)=x+y^2-3$
- $g(x,y)=c$ - the constraint - $g(x,y)=2x-4y=12$
- Then solve $\vec \nabla f = \lambda \vec \nabla g$ together with $g(x,y)=c$.
The equation $\vec \nabla f = \lambda \vec \nabla g$ gives $(1,2y) = \lambda(2,-4)$, which means $1=2\lambda$ and $2y = -4\lambda$. The first equation means $\lambda = \frac{1}{2}$, which means $y=-1$ from the second equation. Plugging $y=-1$ into $2x-4y=12$ yields $x=4$.
We can check our work, as well as visualize what is happening, with the following Mathematica notebook.
- Imagine a rover follows a linear path through some terrain whose contour plot is given below.
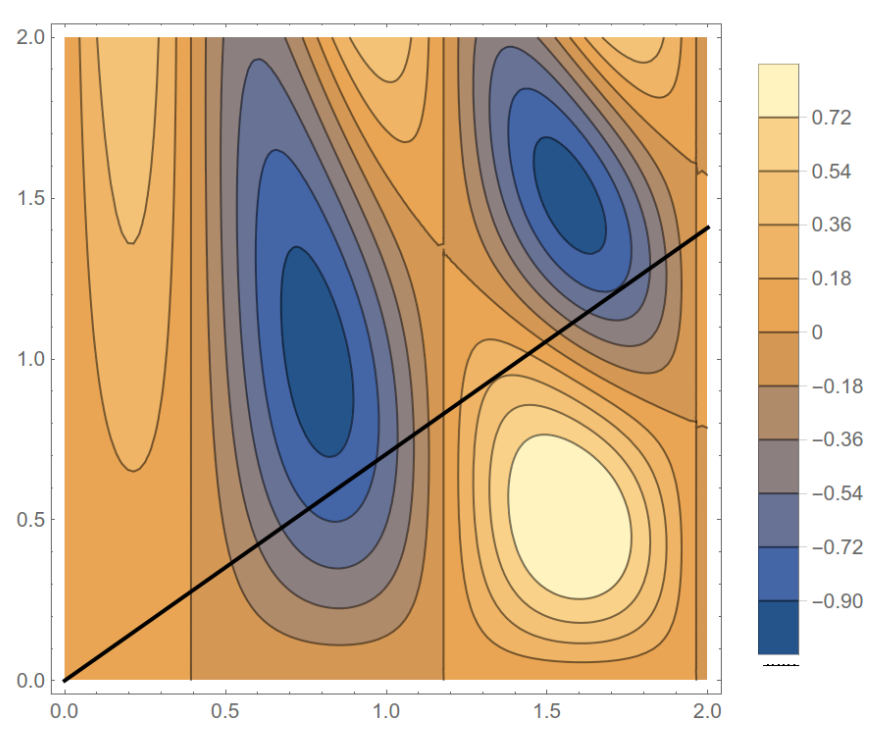
Identify the points that the Lagrange multipliers process will yield.
Solution
We'll discuss this in class. There are 4 points, namely the places where the path would meet a level curve tangentially. The one in the lower left corner is very subtle. Not all level curves are drawn, so we have to estimate some of these points.
- The US mint creates coins that are roughly a cylindrical shape, with volume $V = \pi r^2h$. Unfortunately, not every coin is exactly the same size, and small errors in $r$ (given by $dr$) and small errors in $h$ (given by $dh$), affect the amount of material needed to mint these coins. The radius of a coin is much larger than the height. Will an error in the radius, or an error in the height, cause a larger change in volume? Explain using differentials.
Solution
An error in height will cause a larger change in volume.
We have $dV = 2\pi rh dr + \pi r^2 dh$. Note that an error in $r$ will be multiplied by $2\pi rh$, while an error in $h$ will be multiplied by $\pi r^2$. Because $r$ is much larger than $h$, then $\pi r^2>2\pi rh$, which means the error $dh$ will be multiplied by the larger value, resulting in a larger change in $V$.
We could pick some simple values to do the comparison. Let $h=1$ and $r=10$ (much larger). We then have $dV = 20\pi dr + 100\pi dh$. Note that an error in $h$ is multiplied by $100\pi$, while an error in $r$ is multiplied by just $20\pi$.
Group Problems
- Suppose $h$ is a function of $p$ and $q$, where $p$ and $q$ are both functions of $x$, $y$, and $z$. Compute the partial derivatives of $h$ with respect to $x$, $y$, and $z$.
- Give an equation of the tangent plane to $xy+z^2=7$ at the point $P=(-3,-2,1)$. [Check: $(-2)(x-(-3))+(-3)(y-(-2))+2(1)(z-1)=0$. ]
- Give an equation of the tangent plane to $z=f(x,y)=xy^2$ at the point $P=(4,-1,f(4,-1))$. [Check: $z-4 = (-1)^2(x-4)+2(4)(-1)(y-(-1))$.]
- Consider the function $f(x,y)= 2x^2+3xy+4y^2-5x+2y$.
- Find all critical points of $f$. [Check: $(x,y) = (2,-1)$.]
- Determine the eigenvalues of the second derivative at each critical point. [Check: The eigenvalues are $\lambda = 6\pm\sqrt{13}$, so $\lambda \approx 9.6$ or $\lambda \approx 2.4$.]
- At each critical point, do we have a local max, local min, or saddle?
- A rover travels along the curve $x^2y=16$ with $x>0$. The elevation near the rover is given by $z=-x^2-y^2$. Locate the $(x,y)$ coordinates where the rover reaches maximum height. [Check: You should obtain $y=2$ and two different $x$ values, giving two solutions.]
