Brain Gains (Rapid Recall, Jivin' Generation)

- Below are several vector field plots. Associated with each vector field plot are two numbers, called eigenvalues (which we will soon learn to compute). What patterns do you see between the vector field plots and the eigenvalues.
Expand to see the plots.

- Let $A(r,h) = 2rh+\frac{1}{2}\pi r^2$. This function gives the area of a region in the plane of a rectangle with side lengths $2r$ and $h$, attached to a semicircle of radius $r$. The radius is supposed to be $r=4$ with $h=3$. Use differentials to estimate the change in area $dA$ that would result from a change in $r$ of $dr = 0.1$ and change in $h$ of $dh = 0.5$.
- Let $f(x,y) = 3xy+\frac{1}{2}x^2$ represent the elevation of a rover near some point on Mars (with (0,0) corresponding to the landing spot). The rover is currently at $(4,3)$. What is the slope of the terrain at the rover's location in the $(1,5)$ direction (so slightly east of north). In other words, compute the directional derivative of $f$ at point $(4,3)$ in the direction $(1,5)$, written as $D_{ (1,5) }f(4,3)$.
- The image below shows a contour plot of a function $f$. Add $\vec \nabla f$ to several points on the plot. Add at least two vectors, one where the gradient should be long, and another where the gradient should be short.
Expand to see the plot.
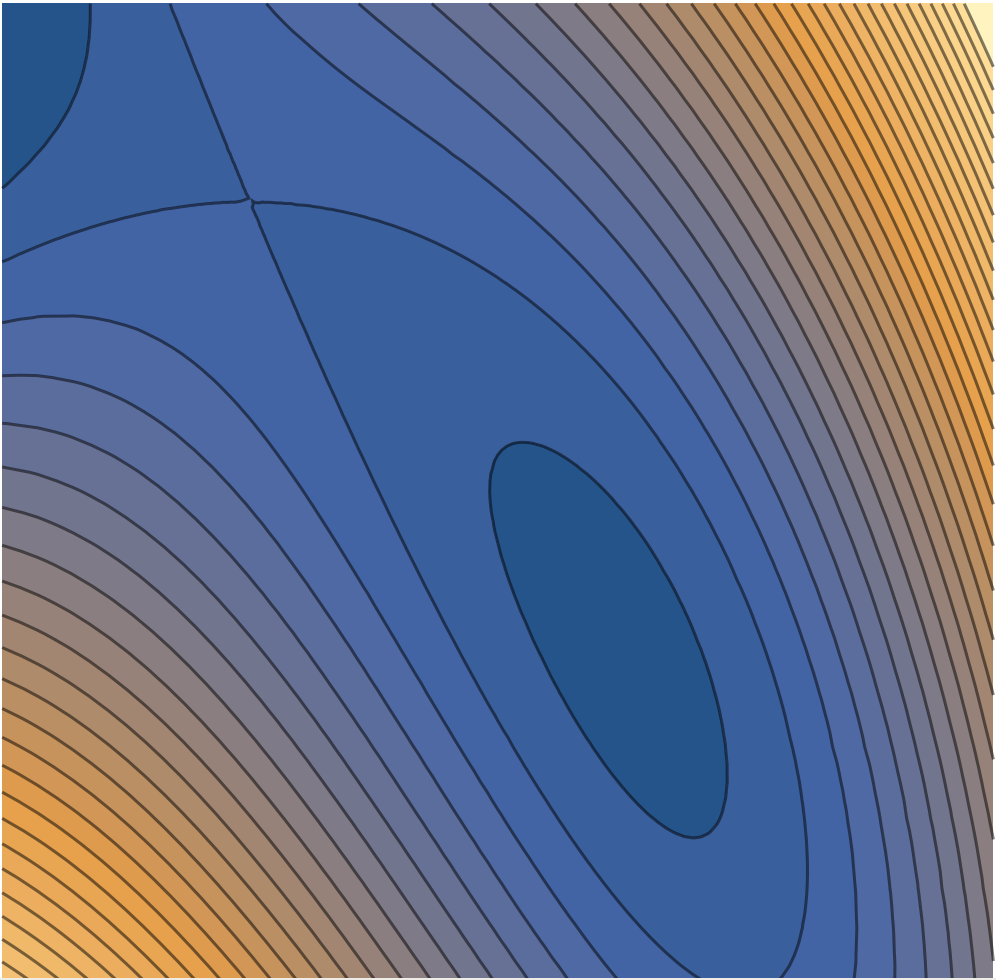
Group Problems
- Let $g(x,y) =xy^3$.
- State $g_x$ and $\dfrac{\partial g}{\partial y}$. Then state $\vec \nabla g$.
- The formula for the directional derivative of $f$ at $P$ in the direction $\vec u$ is $D_{\vec u}f(P) = \vec \nabla f(P)\cdot \dfrac{\vec u}{|\vec u|}$. For this function $g$, verify that the directional derivative of $g$ at $(x,y)$ in the direction $(1,0)$ is indeed $g_x$.
- Find the directional derivative (slope) of $g$ at $P=(3,1)$ in the direction $(-3,2)$.
- Find the directional derivative of $g$ at $P=(3,1)$ in the direction $(2,-5)$.
- Consider the elevation function $f(x,y)=e^x\sin y$ and the path $\vec r(t) = (t^2,t^3)$.
- Compute $f(\vec r(t))$ and then compute $\frac{df}{dt}$.
- Find $df$ in terms of $x$, $y$, $dx$, and $dy$. Then find $dx$ and $dy$ in terms of $t$ and $dt$.
- Use substitution to state $df$ in terms of $dt$ and divide by $dt$ to obtain $\frac{df}{dt}$. [You should have the same answer as the first part.]
- In your solution for $\frac{df}{dt}$, label each of $f_x$, $f_y$, $\frac{dx}{dt}$ and $\frac{dy}{dt}$ to verify that $$\frac{df}{dt} = f_x\frac{dx}{dt}+f_y\frac{dy}{dt}.$$
- Consider the function $f(x,y,z) = 4x^2+4y^2+z^2$. We'll be analyzing the surface at the point $P=(1/2,0,\sqrt{3})$.
- Compute $f(1/2,0,\sqrt{3})$.
- Draw the level surface that passes through $(1/2,0,\sqrt{3})$. So draw the ellipsoid $4=4x^2+4y^2+z^2$, which we can rewrite at $1=x^2+y^2+\frac{z^2}{4}$.
- Compute the gradient $\vec\nabla f(x,y,z)$, and then give $\vec\nabla f(P)$.
- Compute the differential $df$, and then the differential at $P$. [Check: For the latter, $df = 4dx+0dy+2\sqrt{3}dz$]
- For a level surface, the output remains constant (so $df=0$). If we let $(x,y,z)$ be a point on the surface really close to $P$, then we have $dx=x-1/2$, $dy=y-0$ and $dz = z-?$. Plug this information into the differential at $P$ to obtain an equation of the tangent plane to the surface.
- Give an equation of the tangent plane to the level surface of $f$ that passes through $(1,2,-3)$.
- Give an equation of the tangent plane to the level surface of $f$ that passes through $(a,b,c)$.
- Consider the function $f(x,y)=2-|x|$.
- Construct a 2D contour plot. Label your contours with their corresponding height.
- Construct a 3D surface plot.
- Construct both the above with software.
